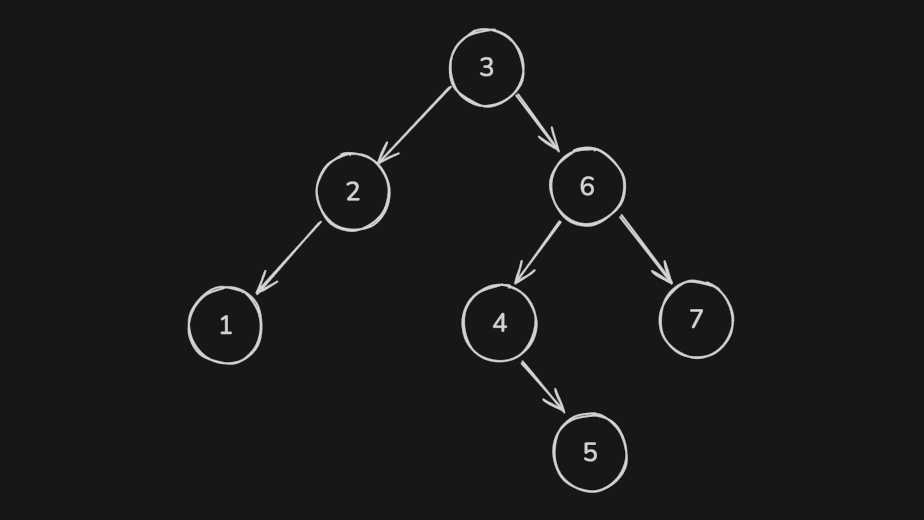
Binary Search Trees
Background
Binary search trees (BSTs) offer an efficient way to insert, remove, and query unordered data in a collection. BSTs, specifically their balanced counterparts, are commonly used in heaps, routing tables, and abstract data structures such as sets.
Time Complexity
| Operation | Average Time | Worst Time |
|---|---|---|
| Insertion | log(n) | n |
| Deletion | log(n) | n |
| Search | log(n) | n |
Binary Search Trees
BSTs are composed of nodes that hold a value and pointers to other nodes. Specifically, each node has a left and a right pointer. Every node must satisfy the constraint that all nodes to the left of it have a value less than its value, and all nodes to the right have a value greater than its value.
struct node {
int data;
struct node *left;
struct node *right;
};Insertion
To insert a new node, we start at the root and traverse down the tree, comparing the new value with the current node’s value. If the new value is smaller, we go left; if it’s larger, we go right. We continue this process until we find an empty spot where the new node can be inserted as a leaf.
function insert(node, value):
if node is null:
return create_node(value)
if value < node.value:
node.left = insert(node.left, value)
else if value > node.value:
node.right = insert(node.right, value)
return nodeDeletion
Deleting a node is more complex and depends on the number of children the node has:
- Node with no children (leaf node): Simply remove the node.
- Node with one child: Replace the node with its child.
- Node with two children: Find the in-order successor (the smallest node in the right subtree) or the in-order predecessor (the largest node in the left subtree). Copy its value to the node to be deleted, and then delete the successor/predecessor.
function delete(node, value):
if node is null: return null
if value < node.value:
node.left = delete(node.left, value)
else if value > node.value:
node.right = delete(node.right, value)
else:
if node.left is null:
return node.right
else if node.right is null:
return node.left
min_larger_node = find_min(node.right)
node.value = min_larger_node.value
node.right = delete(node.right, min_larger_node.value)
return nodeSearch
Searching for a value is similar to insertion. We start at the root and compare the target value with the current node’s value. If they are equal, we’ve found the node. If the target is smaller, we search the left subtree. If it’s larger, we search the right subtree. If we reach a null pointer, the value is not in the tree.
function search(node, value):
if node is null or node.value == value:
return node
if value < node.value:
return search(node.left, value)
else:
return search(node.right, value)Implementation
For the complete C implementation, see this repository.
Conclusion
Binary search trees are a fundamental data structure with a wide range of applications. While they are simple to implement and offer excellent average-case performance, their performance can degrade to that of a linked list in the worst case (e.g., when inserting sorted data).
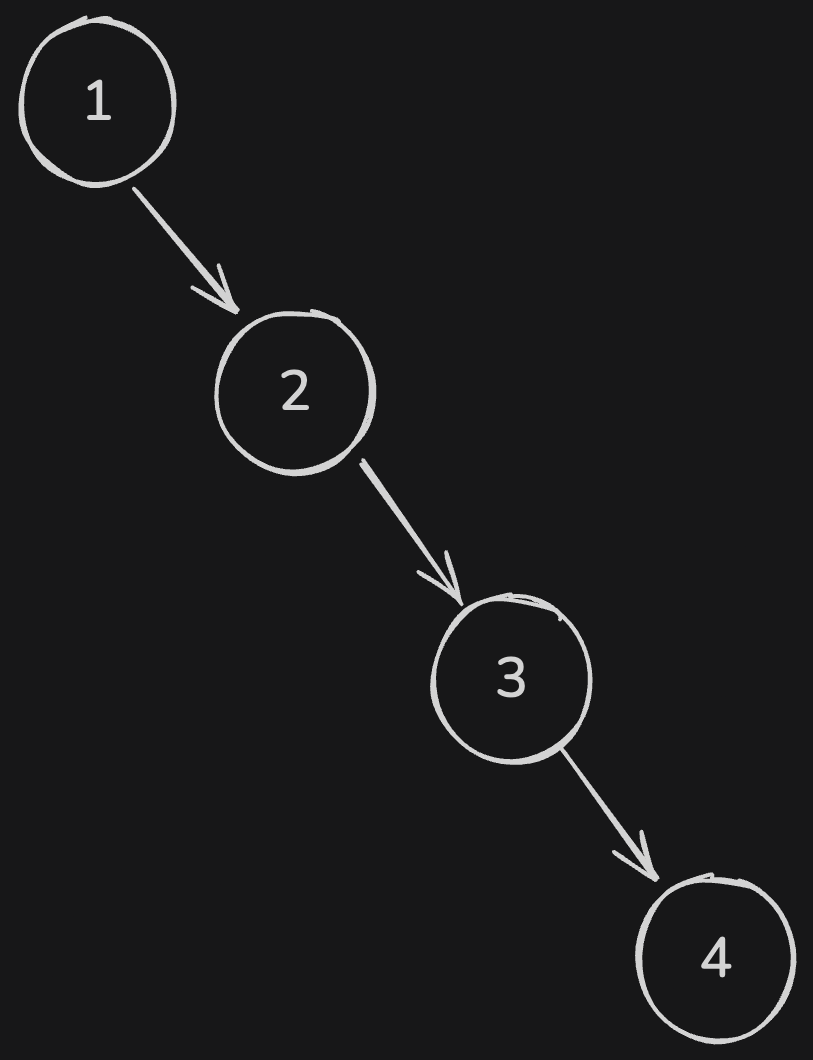
To overcome this, self-balancing BSTs like AVL trees or Red-Black trees are often used in practice to guarantee logarithmic time complexity for all operations.